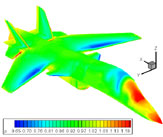
Меньшов Игорь Станиславович

Образование и работа

Ведущий научный сотрудник Института прикладной математики им. М.В. Келдыша РАН, доктор физ.-мат. наук, окончил мех-мат МГУ в 1979 г., аспирантуру Математического института им. В.А. Стеклова АН СССР в 1982 г.

Кандидатская диссертация — «Нестационарные течения дисперсных сред», 1982 г.

Докторская диссертация — «Метод обобщенной задачи Римана в вычислительной гидродинамике», 2007 г.

Работал в университете г. Нагоя, Япония: Assistant Professor (1994—1996 гг.), лектор (1998—2001 гг.), профессор (2001—2007 гг.).

Область научных исследований

Прикладная газодинамика, аэродинамика, численные методы механики сжимаемой жидкости, методы математического моделирования в гидродинамике, аэроакустика, неустойчивость и турбулентность, течения в пористых средах.

Краткая характеристика научных результатов

Выполнено полное исследование обобщенной (неавтомодельной) задачи Римана о распаде произвольного разрыва в неоднородном газе. Как в одномерном приближении, так и в общем (многомерном) случае, доказана ее корректность, получены точные решения.

Аналогичная задача рассмотрена для стационарных уравнений сверхзвуковой газодинамики (неавтомодельная задача о взаимодействии двух неоднородных по пространству сверхзвуковых потоков). Найдено ее решение в форме конечных аналитических выражений.

Разработан метод обобщенной задачи Римана, который фактически является первой последовательной модификацией численного метода Годунова на случай сеточных восполнений повышенного порядка точности (кусочно-линейных и выше). Метод реализован для нестационарных уравнений газовой динамики, а также для стационарных сверхзвуковых уравнений.

Дана постановка и проведено полное исследование вариационной задачи Римана — задачи о первой вариации решения римановской автомодельной задачи по отношению к малым вариациям начальных данных. Доказано существование и единственность решения при произвольных начальных вариациях. Выписано общее решение в виде явных функций начальных данных.

Проведена точная линеаризация функции годуновского численного потока и построен неявный аналог схемы С. К. Годунова, обеспечивающий значительное ускорение сходимости численных решений.

На основе решения вариационной задачи Римана разработана численная методика, являющаяся обобщением метода С. К. Годунова на задачи аэроакустики. Она позволяет рассчитывать эволюцию полей малых возмущений на фоне неоднородных течений газа, в том числе при наличии в потоке сильных разрывов.

Получен также ряд результатов, касающихся следующих задач:

• распространение ударных и детонационных волн в пылегазовых смесях;
• гибридные явно-неявные схемы интегрирования по времени для систем гиперболических уравнений, обеспечивающие абсолютную устойчивость при минимальной диссипации;
• гиперзвуковая аэродинамика в условиях химического и термодинамического неравновесия;
• гидродинамическая неустойчивость вихревых и струйных течений;
• численное моделирование физико-химических процессов внутренней баллистики (горение газопороховых смесей).

Награды

Премия и золотая медаль АН СССР молодым ученым за лучшую научную работу (1989). Первая премия инженерного общества Японии за лучшую работу в области образования (2005).

Педагогическая деятельность

• курс лекций «Современные численные методы газовой динамики»
• руководитель курсовых и дипломных работ студентов кафедры

Темы для третьекурсников

Темы курсовых работ так или иначе связаны с постановкой и проведением вычислительного эксперимента в области аэродинамики, механики сжимаемой жидкости. Они охватывают разработку современных вычислительных технологий, в том числе ориентированных на использование высокопроизводительных многопроцессорных вычислительных систем. Список примерных тем включает в себя следующие:

• неустойчивость и аэроакустика течения газовой струи;
• газодинамика и динамика деформируемого тела;
• виброакустика;
• газодинамика с учетом многокомпонентности, неравновесности, химических реакций;
• многофазные течения, в том числе задачи внутренней баллистики;
• аэродинамика около пористых (проницаемых) поверхностей;
• сопряженные задачи аэродинамики и динамики твердого тела.

Публикации

Автор более 100 научных работ и одного учебного пособия. [Список публикаций]

Координаты

 250-78-83, +7 906 067-11-01

 menshov@kiam.ru, imen57@mail.ru